- 참고 : 핸즈온 머신러닝 2판
- 다변량 회귀 : 독립변수가 둘 이상인 회귀 문제
- 단변량 회귀 : 독립변수가 하나인 회귀 문제
- 회귀 성능지표
- RMSE (평균 제곱근 오차) - 오차가 커질수록 값이 커짐
- MAE (평균 절대 오차) - 이상치에 민감한 성능지표
둘다 예측값과 target값 사이의 거리를 재는 방법
데이터 구조 훑어 보기
housing = load_housing_data()
housing.head()| longitude | latitude | housing_median_age | total_rooms | total_bedrooms | population | households | median_income | median_house_value | ocean_proximity | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | -122.23 | 37.88 | 41.0 | 880.0 | 129.0 | 322.0 | 126.0 | 8.3252 | 452600.0 | NEAR BAY |
| 1 | -122.22 | 37.86 | 21.0 | 7099.0 | 1106.0 | 2401.0 | 1138.0 | 8.3014 | 358500.0 | NEAR BAY |
| 2 | -122.24 | 37.85 | 52.0 | 1467.0 | 190.0 | 496.0 | 177.0 | 7.2574 | 352100.0 | NEAR BAY |
| 3 | -122.25 | 37.85 | 52.0 | 1274.0 | 235.0 | 558.0 | 219.0 | 5.6431 | 341300.0 | NEAR BAY |
| 4 | -122.25 | 37.85 | 52.0 | 1627.0 | 280.0 | 565.0 | 259.0 | 3.8462 | 342200.0 | NEAR BAY |
housing.columns
>> Index(['longitude', 'latitude', 'housing_median_age', 'total_rooms',
'total_bedrooms', 'population', 'households', 'median_income',
'median_house_value', 'ocean_proximity'],
dtype='object')- 데이터에서 각 행이 하나의 구역을 의미
- 특성은 10개
'longitude', 'latitude', 'housing_median_age', 'total_rooms', 'total_bedrooms', 'population', 'households', 'median_income', 'median_house_value', 'ocean_proximity'- target은 income_cat
housing.info()
>> <class 'pandas.core.frame.DataFrame'>
RangeIndex: 20640 entries, 0 to 20639
Data columns (total 10 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 longitude 20640 non-null float64
1 latitude 20640 non-null float64
2 housing_median_age 20640 non-null float64
3 total_rooms 20640 non-null float64
4 total_bedrooms 20433 non-null float64
5 population 20640 non-null float64
6 households 20640 non-null float64
7 median_income 20640 non-null float64
8 median_house_value 20640 non-null float64
9 ocean_proximity 20640 non-null object
dtypes: float64(9), object(1)
memory usage: 1.6+ MB- info()를 통해 데이터 타입, 수, nan 파악이 용이
housing["ocean_proximity"].value_counts()
>> <1H OCEAN 9136
INLAND 6551
NEAR OCEAN 2658
NEAR BAY 2290
ISLAND 5
Name: ocean_proximity, dtype: int64housing.describe()| longitude | latitude | housing_median_age | total_rooms | total_bedrooms | population | households | median_income | median_house_value | |
|---|---|---|---|---|---|---|---|---|---|
| count | 20640.000000 | 20640.000000 | 20640.000000 | 20640.000000 | 20433.000000 | 20640.000000 | 20640.000000 | 20640.000000 | 20640.000000 |
| mean | -119.569704 | 35.631861 | 28.639486 | 2635.763081 | 537.870553 | 1425.476744 | 499.539680 | 3.870671 | 206855.816909 |
| std | 2.003532 | 2.135952 | 12.585558 | 2181.615252 | 421.385070 | 1132.462122 | 382.329753 | 1.899822 | 115395.615874 |
| min | -124.350000 | 32.540000 | 1.000000 | 2.000000 | 1.000000 | 3.000000 | 1.000000 | 0.499900 | 14999.000000 |
| 25% | -121.800000 | 33.930000 | 18.000000 | 1447.750000 | 296.000000 | 787.000000 | 280.000000 | 2.563400 | 119600.000000 |
| 50% | -118.490000 | 34.260000 | 29.000000 | 2127.000000 | 435.000000 | 1166.000000 | 409.000000 | 3.534800 | 179700.000000 |
| 75% | -118.010000 | 37.710000 | 37.000000 | 3148.000000 | 647.000000 | 1725.000000 | 605.000000 | 4.743250 | 264725.000000 |
| max | -114.310000 | 41.950000 | 52.000000 | 39320.000000 | 6445.000000 | 35682.000000 | 6082.000000 | 15.000100 | 500001.000000 |
%matplotlib inline
import matplotlib.pyplot as plt
housing.hist(bins=50, figsize=(20,15))
save_fig("attribute_histogram_plots")
plt.show()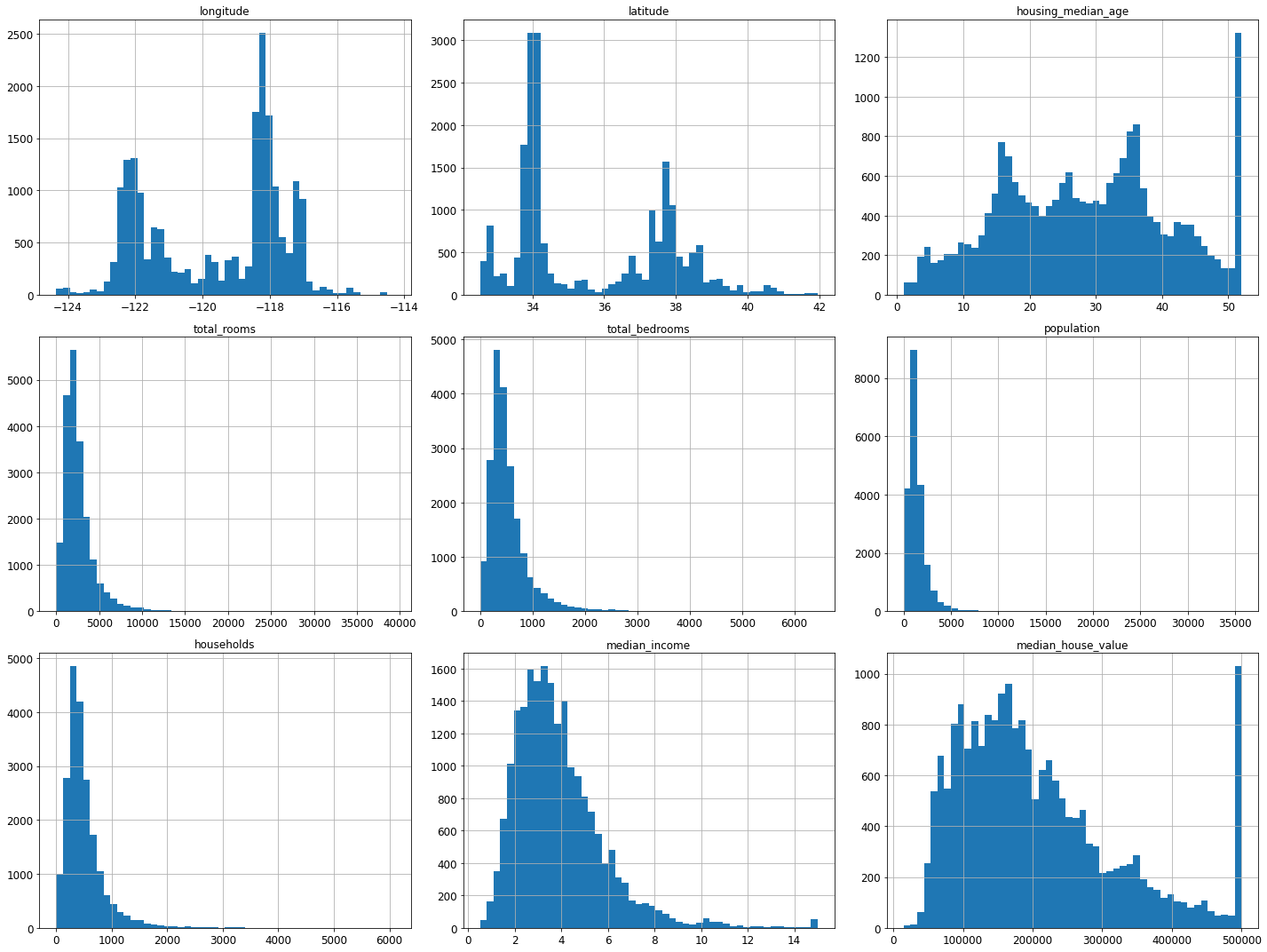
테스트 세트 만들기
from sklearn.model_selection import train_test_split
train_set, test_set = train_test_split(housing, test_size=0.2, random_state=42)
test_set.head()| longitude | latitude | housing_median_age | total_rooms | total_bedrooms | population | households | median_income | median_house_value | ocean_proximity | |
|---|---|---|---|---|---|---|---|---|---|---|
| 20046 | -119.01 | 36.06 | 25.0 | 1505.0 | NaN | 1392.0 | 359.0 | 1.6812 | 47700.0 | INLAND |
| 3024 | -119.46 | 35.14 | 30.0 | 2943.0 | NaN | 1565.0 | 584.0 | 2.5313 | 45800.0 | INLAND |
| 15663 | -122.44 | 37.80 | 52.0 | 3830.0 | NaN | 1310.0 | 963.0 | 3.4801 | 500001.0 | NEAR BAY |
| 20484 | -118.72 | 34.28 | 17.0 | 3051.0 | NaN | 1705.0 | 495.0 | 5.7376 | 218600.0 | <1H OCEAN |
| 9814 | -121.93 | 36.62 | 34.0 | 2351.0 | NaN | 1063.0 | 428.0 | 3.7250 | 278000.0 | NEAR OCEAN |
housing["median_income"].hist()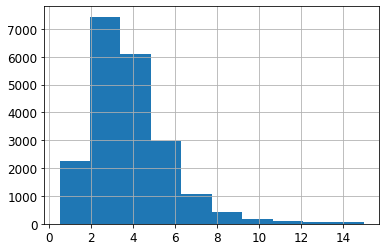
- pd.cut()을 통한 카테고리 5개의 소득 특성을 생성
housing["income_cat"] = pd.cut(housing["median_income"],
bins=[0., 1.5, 3.0, 4.5, 6., np.inf],
labels=[1, 2, 3, 4, 5])
housing["income_cat"].value_counts()
>> 3 7236
2 6581
4 3639
5 2362
1 822
Name: income_cat, dtype: int64housing["income_cat"].hist()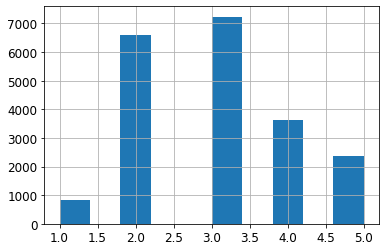
- StratifiedShuffleSplit : stratifiedkfold의 계층 샘플링, shufflesplit 랜덤 샘플링을 합친 것
from sklearn.model_selection import StratifiedShuffleSplit
split = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=42)
for train_index, test_index in split.split(housing, housing["income_cat"]):
strat_train_set = housing.loc[train_index]
strat_test_set = housing.loc[test_index]- test_set의 소득 카테고리의 비율 확인
strat_test_set["income_cat"].value_counts() / len(strat_test_set)
>> 3 0.350533
2 0.318798
4 0.176357
5 0.114341
1 0.039971
Name: income_cat, dtype: float64housing["income_cat"].value_counts() / len(housing)
>> 3 0.350581
2 0.318847
4 0.176308
5 0.114438
1 0.039826
Name: income_cat, dtype: float64def income_cat_proportions(data):
return data["income_cat"].value_counts() / len(data)
train_set, test_set = train_test_split(housing, test_size=0.2, random_state=42)
compare_props = pd.DataFrame({
"전체": income_cat_proportions(housing),
"계층 샘플링": income_cat_proportions(strat_test_set),
"무작위 샘플링": income_cat_proportions(test_set),
}).sort_index()
compare_props["무작위 샘플링 오류"] = 100 * compare_props["무작위 샘플링"] / compare_props["전체"] - 100
compare_props["계층 샘플링 오류"] = 100 * compare_props["계층 샘플링"] / compare_props["전체"] - 100- 전체 데이터셋과 계층 샘플링으로 만든 테스트 세트에서 소득 카테고리 비율을 비교한 것
compare_props| 전체 | 계층 샘플링 | 무작위 샘플링 | 무작위 샘플링 오류 | 계층 샘플링 오류 | |
|---|---|---|---|---|---|
| 1 | 0.039826 | 0.039971 | 0.040213 | 0.973236 | 0.364964 |
| 2 | 0.318847 | 0.318798 | 0.324370 | 1.732260 | -0.015195 |
| 3 | 0.350581 | 0.350533 | 0.358527 | 2.266446 | -0.013820 |
| 4 | 0.176308 | 0.176357 | 0.167393 | -5.056334 | 0.027480 |
| 5 | 0.114438 | 0.114341 | 0.109496 | -4.318374 | -0.084674 |
```python for set_ in (strat_train_set, strat_test_set): set_.drop("income_cat", axis=1, inplace=True) ```
데이터 이해를 위한 탐색과 시각화
지리적 데이터 시각화
- 위도, 경도 데이터를 사용해 모든 구역을 산점도로 시각화
housing = strat_train_set.copy()
housing.plot(kind="scatter", x="longitude", y="latitude")
save_fig("bad_visualization_plot")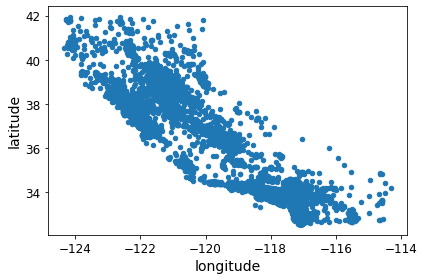
- alpha 값을 줘서 밀집영역 확인이 용이
housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.1)
save_fig("better_visualization_plot")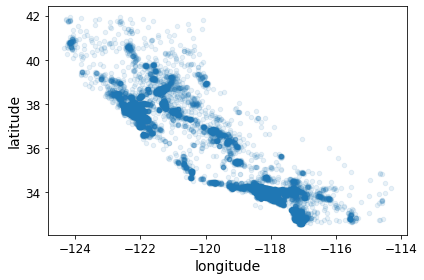
- 원의 반지름은 구역의 인구를 의미
- 색상은 가격을 의미
- 군집알고리즘으로 주요 군집의 특징을 찾을수도 있음
housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.4,
s=housing["population"]/100, label="population", figsize=(10,7),
c="median_house_value", cmap=plt.get_cmap("jet"), colorbar=True,
sharex=False)
plt.legend()
save_fig("housing_prices_scatterplot")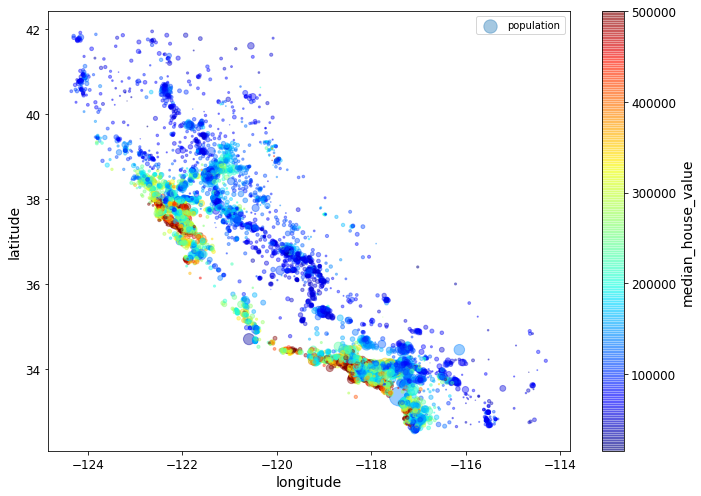
상관관계 조사
- 상관관계의 범위는 -1 ~ 1 까지
- 1에 가까우면 강한 양의 상관관계를 가짐
- 선형적인 상관관계만을 측정가능 비선형적인 관계를 확인할수 없음
corr_matrix = housing.corr()corr_matrix["median_house_value"].sort_values(ascending=False)
>> median_house_value 1.000000
median_income 0.687151
total_rooms 0.135140
housing_median_age 0.114146
households 0.064590
total_bedrooms 0.047781
population -0.026882
longitude -0.047466
latitude -0.142673
Name: median_house_value, dtype: float64- 다른 수치형 특성에 대한 각 수치형 특성의 산점도와 각 수치형 특성의 히스토그램을 출력
from pandas.plotting import scatter_matrix
attributes = ["median_house_value", "median_income", "total_rooms",
"housing_median_age"]
scatter_matrix(housing[attributes], figsize=(12, 8))
save_fig("scatter_matrix_plot")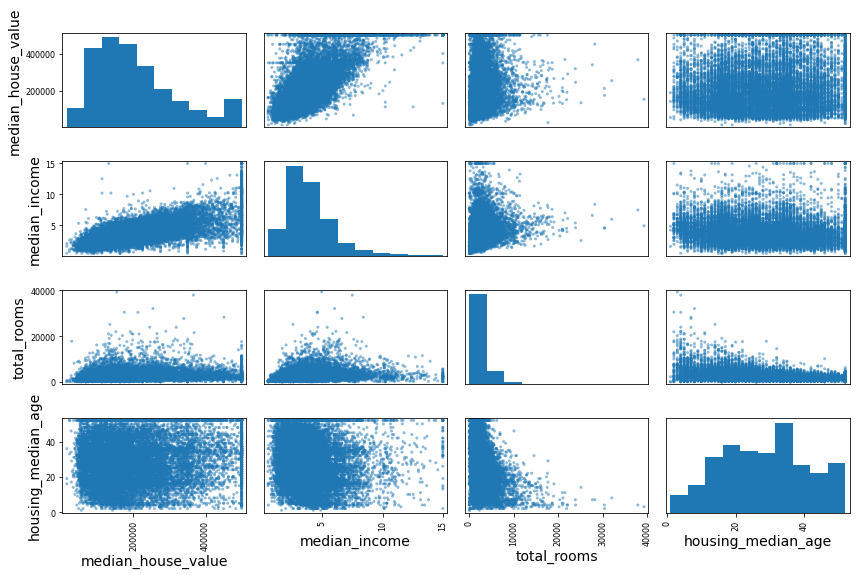
- 강한 상관관계를 띄는 median_income, median_house_value
- 부분적으로 직선형태를 보임 -> 안 좋은 데이터 형태
housing.plot(kind="scatter", x="median_income", y="median_house_value",
alpha=0.1)
plt.axis([0, 16, 0, 550000])
save_fig("income_vs_house_value_scatterplot")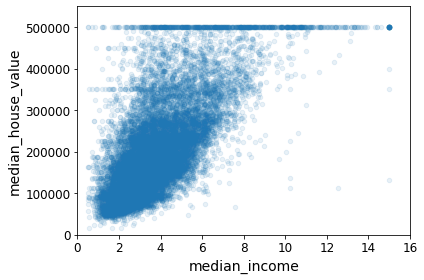
특성 조합으로 실험
- 여러가지 특성들을 합쳐서 새로운 특성을 생성
housing["rooms_per_household"] = housing["total_rooms"]/housing["households"]
housing["bedrooms_per_room"] = housing["total_bedrooms"]/housing["total_rooms"]
housing["population_per_household"]=housing["population"]/housing["households"]corr_matrix = housing.corr()
corr_matrix["median_house_value"].sort_values(ascending=False)
>> median_house_value 1.000000
median_income 0.687151
rooms_per_household 0.146255
total_rooms 0.135140
housing_median_age 0.114146
households 0.064590
total_bedrooms 0.047781
population_per_household -0.021991
population -0.026882
longitude -0.047466
latitude -0.142673
bedrooms_per_room -0.259952
Name: median_house_value, dtype: float64housing.plot(kind="scatter", x="rooms_per_household", y="median_house_value",
alpha=0.2)
plt.show()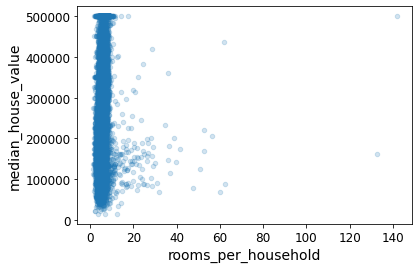
housing.describe()| longitude | latitude | housing_median_age | total_rooms | total_bedrooms | population | households | median_income | median_house_value | rooms_per_household | bedrooms_per_room | population_per_household | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 16512.000000 | 16512.000000 | 16512.000000 | 16512.000000 | 16354.000000 | 16512.000000 | 16512.000000 | 16512.000000 | 16512.000000 | 16512.000000 | 16354.000000 | 16512.000000 |
| mean | -119.575635 | 35.639314 | 28.653404 | 2622.539789 | 534.914639 | 1419.687379 | 497.011810 | 3.875884 | 207005.322372 | 5.440406 | 0.212873 | 3.096469 |
| std | 2.001828 | 2.137963 | 12.574819 | 2138.417080 | 412.665649 | 1115.663036 | 375.696156 | 1.904931 | 115701.297250 | 2.611696 | 0.057378 | 11.584825 |
| min | -124.350000 | 32.540000 | 1.000000 | 6.000000 | 2.000000 | 3.000000 | 2.000000 | 0.499900 | 14999.000000 | 1.130435 | 0.100000 | 0.692308 |
| 25% | -121.800000 | 33.940000 | 18.000000 | 1443.000000 | 295.000000 | 784.000000 | 279.000000 | 2.566950 | 119800.000000 | 4.442168 | 0.175304 | 2.431352 |
| 50% | -118.510000 | 34.260000 | 29.000000 | 2119.000000 | 433.000000 | 1164.000000 | 408.000000 | 3.541550 | 179500.000000 | 5.232342 | 0.203027 | 2.817661 |
| 75% | -118.010000 | 37.720000 | 37.000000 | 3141.000000 | 644.000000 | 1719.000000 | 602.000000 | 4.745325 | 263900.000000 | 6.056361 | 0.239816 | 3.281420 |
| max | -114.310000 | 41.950000 | 52.000000 | 39320.000000 | 6210.000000 | 35682.000000 | 5358.000000 | 15.000100 | 500001.000000 | 141.909091 | 1.000000 | 1243.333333 |
머신러닝 알고리즘을 위한 데이터 준비
- 데이터 준비를 자동화하는 이유
- 어떤 데이터셋에 대해서도 데이터 변환을 손쉽게 반복가능
- 향후 프로젝트에 사용할 수 있는 변환 라이브러리를 점진적으로 구축
- 실제 시스템에서 알고리즘에 새 데이터를 주입하기 전에 변환시키는데 사용가능
- 여러 가지 데이터 변환을 쉽게 시도가능, 어떤 조합이 가장 좋은지 확인하는 데 편리함
housing = strat_train_set.drop("median_house_value", axis=1) # 훈련 세트를 위해 레이블 삭제
housing_labels = strat_train_set["median_house_value"].copy()데이터 정제
책에 소개된 세 개의 옵션은 다음과 같습니다:
housing.dropna(subset=["total_bedrooms"]) # 옵션 1
housing.drop("total_bedrooms", axis=1) # 옵션 2
median = housing["total_bedrooms"].median() # 옵션 3
housing["total_bedrooms"].fillna(median, inplace=True)각 옵션을 설명하기 위해 주택 데이터셋의 복사본을 만듭니다. 이 때 적어도 하나의 열이 비어 있는 행만 고릅니다. 이렇게 하면 각 옵션의 정확한 동작을 눈으로 쉽게 확인할 수 있습니다.
sample_incomplete_rows = housing[housing.isnull().any(axis=1)].head()
sample_incomplete_rows| longitude | latitude | housing_median_age | total_rooms | total_bedrooms | population | households | median_income | ocean_proximity | |
|---|---|---|---|---|---|---|---|---|---|
| 1606 | -122.08 | 37.88 | 26.0 | 2947.0 | NaN | 825.0 | 626.0 | 2.9330 | NEAR BAY |
| 10915 | -117.87 | 33.73 | 45.0 | 2264.0 | NaN | 1970.0 | 499.0 | 3.4193 | <1H OCEAN |
| 19150 | -122.70 | 38.35 | 14.0 | 2313.0 | NaN | 954.0 | 397.0 | 3.7813 | <1H OCEAN |
| 4186 | -118.23 | 34.13 | 48.0 | 1308.0 | NaN | 835.0 | 294.0 | 4.2891 | <1H OCEAN |
| 16885 | -122.40 | 37.58 | 26.0 | 3281.0 | NaN | 1145.0 | 480.0 | 6.3580 | NEAR OCEAN |
```python sample_incomplete_rows.dropna(subset=["total_bedrooms"]) # 옵션 1 - NAN 값 제거 total_bedrooms 열에 대해서 ```
| longitude | latitude | housing_median_age | total_rooms | total_bedrooms | population | households | median_income | ocean_proximity |
|---|
sample_incomplete_rows.drop("total_bedrooms", axis=1) # 옵션 2 - 열삭제| longitude | latitude | housing_median_age | total_rooms | population | households | median_income | ocean_proximity | |
|---|---|---|---|---|---|---|---|---|
| 1606 | -122.08 | 37.88 | 26.0 | 2947.0 | 825.0 | 626.0 | 2.9330 | NEAR BAY |
| 10915 | -117.87 | 33.73 | 45.0 | 2264.0 | 1970.0 | 499.0 | 3.4193 | <1H OCEAN |
| 19150 | -122.70 | 38.35 | 14.0 | 2313.0 | 954.0 | 397.0 | 3.7813 | <1H OCEAN |
| 4186 | -118.23 | 34.13 | 48.0 | 1308.0 | 835.0 | 294.0 | 4.2891 | <1H OCEAN |
| 16885 | -122.40 | 37.58 | 26.0 | 3281.0 | 1145.0 | 480.0 | 6.3580 | NEAR OCEAN |
median = housing["total_bedrooms"].median()
sample_incomplete_rows["total_bedrooms"].fillna(median, inplace=True) # 옵션 3 - nan 값을 mean 값으로 대체sample_incomplete_rows| longitude | latitude | housing_median_age | total_rooms | total_bedrooms | population | households | median_income | ocean_proximity | |
|---|---|---|---|---|---|---|---|---|---|
| 1606 | -122.08 | 37.88 | 26.0 | 2947.0 | 433.0 | 825.0 | 626.0 | 2.9330 | NEAR BAY |
| 10915 | -117.87 | 33.73 | 45.0 | 2264.0 | 433.0 | 1970.0 | 499.0 | 3.4193 | <1H OCEAN |
| 19150 | -122.70 | 38.35 | 14.0 | 2313.0 | 433.0 | 954.0 | 397.0 | 3.7813 | <1H OCEAN |
| 4186 | -118.23 | 34.13 | 48.0 | 1308.0 | 433.0 | 835.0 | 294.0 | 4.2891 | <1H OCEAN |
| 16885 | -122.40 | 37.58 | 26.0 | 3281.0 | 433.0 | 1145.0 | 480.0 | 6.3580 | NEAR OCEAN |
- 위 과정 옵션3 과 동일한 것을 SimpleImputer로 가능
from sklearn.impute import SimpleImputer
imputer = SimpleImputer(strategy="median")- 중간값이 수치형 특성에서만 계산될 수 있기 때문에 텍스트 특성을 삭제합니다:
housing_num = housing.drop("ocean_proximity", axis=1)imputer.fit(housing_num)
SimpleImputer(strategy='median')imputer.statistics_
>> array([-118.51 , 34.26 , 29. , 2119. , 433. ,
1164. , 408. , 3.54155])- 훈련 세트로 변환
X = imputer.transform(housing_num)
housing_tr = pd.DataFrame(X, columns=housing_num.columns,
index=housing_num.index)
housing_tr.loc[sample_incomplete_rows.index.values]| longitude | latitude | housing_median_age | total_rooms | total_bedrooms | population | households | median_income | |
|---|---|---|---|---|---|---|---|---|
| 1606 | -122.08 | 37.88 | 26.0 | 2947.0 | 433.0 | 825.0 | 626.0 | 2.9330 |
| 10915 | -117.87 | 33.73 | 45.0 | 2264.0 | 433.0 | 1970.0 | 499.0 | 3.4193 |
| 19150 | -122.70 | 38.35 | 14.0 | 2313.0 | 433.0 | 954.0 | 397.0 | 3.7813 |
| 4186 | -118.23 | 34.13 | 48.0 | 1308.0 | 433.0 | 835.0 | 294.0 | 4.2891 |
| 16885 | -122.40 | 37.58 | 26.0 | 3281.0 | 433.0 | 1145.0 | 480.0 | 6.3580 |
imputer.strategy
>> 'median'
housing_tr.head()| longitude | latitude | housing_median_age | total_rooms | total_bedrooms | population | households | median_income | |
|---|---|---|---|---|---|---|---|---|
| 12655 | -121.46 | 38.52 | 29.0 | 3873.0 | 797.0 | 2237.0 | 706.0 | 2.1736 |
| 15502 | -117.23 | 33.09 | 7.0 | 5320.0 | 855.0 | 2015.0 | 768.0 | 6.3373 |
| 2908 | -119.04 | 35.37 | 44.0 | 1618.0 | 310.0 | 667.0 | 300.0 | 2.8750 |
| 14053 | -117.13 | 32.75 | 24.0 | 1877.0 | 519.0 | 898.0 | 483.0 | 2.2264 |
| 20496 | -118.70 | 34.28 | 27.0 | 3536.0 | 646.0 | 1837.0 | 580.0 | 4.4964 |
텍스트와 범주형 특성 다루기
이제 범주형 입력 특성인 ocean_proximity을 전처리합니다:
housing_cat = housing[["ocean_proximity"]]
housing_cat.head(10)| ocean_proximity | |
|---|---|
| 12655 | INLAND |
| 15502 | NEAR OCEAN |
| 2908 | INLAND |
| 14053 | NEAR OCEAN |
| 20496 | <1H OCEAN |
| 1481 | NEAR BAY |
| 18125 | <1H OCEAN |
| 5830 | <1H OCEAN |
| 17989 | <1H OCEAN |
| 4861 | <1H OCEAN |
- OrdinalEncoder : 범주가 하나일때는 문제없음, 두개 이상이면 문제있음
from sklearn.preprocessing import OrdinalEncoder
ordinal_encoder = OrdinalEncoder()
housing_cat_encoded = ordinal_encoder.fit_transform(housing_cat)
housing_cat_encoded[:10]
>> array([[1.],
[4.],
[1.],
[4.],
[0.],
[3.],
[0.],
[0.],
[0.],
[0.]])
ordinal_encoder.categories_
>> [array(['<1H OCEAN', 'INLAND', 'ISLAND', 'NEAR BAY', 'NEAR OCEAN'], dtype=object)]from sklearn.preprocessing import OneHotEncoder
cat_encoder = OneHotEncoder()
housing_cat_1hot = cat_encoder.fit_transform(housing_cat)
housing_cat_1hot
>> <16512x5 sparse matrix of type '<class 'numpy.float64'>'
with 16512 stored elements in Compressed Sparse Row format>OneHotEncoder는 기본적으로 희소 행렬을 반환합니다. 필요하면 toarray() 메서드를 사용해 밀집 배열로 변환할 수 있습니다:
housing_cat_1hot.toarray()
>> array([[0., 1., 0., 0., 0.],
[0., 0., 0., 0., 1.],
[0., 1., 0., 0., 0.],
...,
[1., 0., 0., 0., 0.],
[1., 0., 0., 0., 0.],
[0., 1., 0., 0., 0.]])또는 OneHotEncoder를 만들 때 sparse=False로 지정할 수 있습니다:
cat_encoder = OneHotEncoder(sparse=False)
housing_cat_1hot = cat_encoder.fit_transform(housing_cat)
housing_cat_1hot
>> array([[0., 1., 0., 0., 0.],
[0., 0., 0., 0., 1.],
[0., 1., 0., 0., 0.],
...,
[1., 0., 0., 0., 0.],
[1., 0., 0., 0., 0.],
[0., 1., 0., 0., 0.]])cat_encoder.categories_
>> [array(['<1H OCEAN', 'INLAND', 'ISLAND', 'NEAR BAY', 'NEAR OCEAN'],
dtype=object)]
변환 파이프라인
수치형 특성을 전처리하기 위해 파이프라인을 만듭니다:
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
num_pipeline = Pipeline([
('imputer', SimpleImputer(strategy="median")),
('attribs_adder', CombinedAttributesAdder()),
('std_scaler', StandardScaler()),
])
housing_num_tr = num_pipeline.fit_transform(housing_num)
housing_num_tr
>> array([[-0.94135046, 1.34743822, 0.02756357, ..., 0.01739526,
0.00622264, -0.12112176],
[ 1.17178212, -1.19243966, -1.72201763, ..., 0.56925554,
-0.04081077, -0.81086696],
[ 0.26758118, -0.1259716 , 1.22045984, ..., -0.01802432,
-0.07537122, -0.33827252],
...,
[-1.5707942 , 1.31001828, 1.53856552, ..., -0.5092404 ,
-0.03743619, 0.32286937],
[-1.56080303, 1.2492109 , -1.1653327 , ..., 0.32814891,
-0.05915604, -0.45702273],
[-1.28105026, 2.02567448, -0.13148926, ..., 0.01407228,
0.00657083, -0.12169672]])from sklearn.compose import ColumnTransformer
num_attribs = list(housing_num)
cat_attribs = ["ocean_proximity"]
full_pipeline = ColumnTransformer([
("num", num_pipeline, num_attribs),
("cat", OneHotEncoder(), cat_attribs),
])
housing_prepared = full_pipeline.fit_transform(housing)
housing_prepared
>> array([[-0.94135046, 1.34743822, 0.02756357, ..., 0. ,
0. , 0. ],
[ 1.17178212, -1.19243966, -1.72201763, ..., 0. ,
0. , 1. ],
[ 0.26758118, -0.1259716 , 1.22045984, ..., 0. ,
0. , 0. ],
...,
[-1.5707942 , 1.31001828, 1.53856552, ..., 0. ,
0. , 0. ],
[-1.56080303, 1.2492109 , -1.1653327 , ..., 0. ,
0. , 0. ],
[-1.28105026, 2.02567448, -0.13148926, ..., 0. ,
0. , 0. ]])
housing_prepared.shape
>> (16512, 16)
모델 선택과 훈련
훈련 세트에서 훈련하고 평가하기
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(housing_prepared, housing_labels)# 훈련 샘플 몇 개를 사용해 전체 파이프라인을 적용
some_data = housing.iloc[:5]
some_labels = housing_labels.iloc[:5]
some_data_prepared = full_pipeline.transform(some_data)
print("예측:", lin_reg.predict(some_data_prepared))
>> 예측: [ 85657.90192014 305492.60737488 152056.46122456 186095.70946094
244550.67966089]- 실제 값과 비교
print("레이블:", list(some_labels))
>> 레이블: [72100.0, 279600.0, 82700.0, 112500.0, 238300.0]some_data_prepared
>> array([[-0.94135046, 1.34743822, 0.02756357, 0.58477745, 0.64037127,
0.73260236, 0.55628602, -0.8936472 , 0.01739526, 0.00622264,
-0.12112176, 0. , 1. , 0. , 0. ,
0. ],
[ 1.17178212, -1.19243966, -1.72201763, 1.26146668, 0.78156132,
0.53361152, 0.72131799, 1.292168 , 0.56925554, -0.04081077,
-0.81086696, 0. , 0. , 0. , 0. ,
1. ],
[ 0.26758118, -0.1259716 , 1.22045984, -0.46977281, -0.54513828,
-0.67467519, -0.52440722, -0.52543365, -0.01802432, -0.07537122,
-0.33827252, 0. , 1. , 0. , 0. ,
0. ],
[ 1.22173797, -1.35147437, -0.37006852, -0.34865152, -0.03636724,
-0.46761716, -0.03729672, -0.86592882, -0.59513997, -0.10680295,
0.96120521, 0. , 0. , 0. , 0. ,
1. ],
[ 0.43743108, -0.63581817, -0.13148926, 0.42717947, 0.27279028,
0.37406031, 0.22089846, 0.32575178, 0.2512412 , 0.00610923,
-0.47451338, 1. , 0. , 0. , 0. ,
0. ]])from sklearn.metrics import mean_squared_error
housing_predictions = lin_reg.predict(housing_prepared)
lin_mse = mean_squared_error(housing_labels, housing_predictions)
lin_rmse = np.sqrt(lin_mse)
lin_rmse
>> 68627.87390018745from sklearn.metrics import mean_absolute_error
lin_mae = mean_absolute_error(housing_labels, housing_predictions)
lin_mae
>> 49438.66860915802from sklearn.tree import DecisionTreeRegressor
tree_reg = DecisionTreeRegressor(random_state=42)
tree_reg.fit(housing_prepared, housing_labels)- 과대적합 의심, 오차가 없음
housing_predictions = tree_reg.predict(housing_prepared)
tree_mse = mean_squared_error(housing_labels, housing_predictions)
tree_rmse = np.sqrt(tree_mse)
tree_rmse
>> 0.0
교차 검증을 사용한 평가
- k-fold cross validation
- 훈련 세트를 폴드라 불리는 10개의 서브셋으로 무작위 분리
- 결정 트리 모델을 10번 훈련하고 평가
- 매번 다른 폴드를 선택해 평가에 사용하고 나머지 9개는 훈련에 사용
총 10개의 평가 점수가 담긴 배열 반환
from sklearn.model_selection import cross_val_score
scores = cross_val_score(tree_reg, housing_prepared, housing_labels,
scoring="neg_mean_squared_error", cv=10)
tree_rmse_scores = np.sqrt(-scores) # neg_mean_squared_error 이라서 -을 붙임def display_scores(scores):
print("점수:", scores)
print("평균:", scores.mean())
print("표준 편차:", scores.std())
display_scores(tree_rmse_scores)
>> 점수: [72831.45749112 69973.18438322 69528.56551415 72517.78229792
69145.50006909 79094.74123727 68960.045444 73344.50225684
69826.02473916 71077.09753998]
평균: 71629.89009727491
표준 편차: 2914.035468468928lin_scores = cross_val_score(lin_reg, housing_prepared, housing_labels,
scoring="neg_mean_squared_error", cv=10)
lin_rmse_scores = np.sqrt(-lin_scores)
display_scores(lin_rmse_scores)
>> 점수: [71762.76364394 64114.99166359 67771.17124356 68635.19072082
66846.14089488 72528.03725385 73997.08050233 68802.33629334
66443.28836884 70139.79923956]
평균: 69104.07998247063
표준 편차: 2880.3282098180694- 앙상블 모델 학습 (여러 모델을 모아서 성능 극대화)
from sklearn.ensemble import RandomForestRegressor
forest_reg = RandomForestRegressor(n_estimators=100, random_state=42)
forest_reg.fit(housing_prepared, housing_labels)housing_predictions = forest_reg.predict(housing_prepared)
forest_mse = mean_squared_error(housing_labels, housing_predictions)
forest_rmse = np.sqrt(forest_mse)
forest_rmse
>> 18650.698705770003from sklearn.model_selection import cross_val_score
forest_scores = cross_val_score(forest_reg, housing_prepared, housing_labels,
scoring="neg_mean_squared_error", cv=10)
forest_rmse_scores = np.sqrt(-forest_scores)
display_scores(forest_rmse_scores)
>> 점수: [51559.63379638 48737.57100062 47210.51269766 51875.21247297
47577.50470123 51863.27467888 52746.34645573 50065.1762751
48664.66818196 54055.90894609]
평균: 50435.58092066179
표준 편차: 2203.3381412764606scores = cross_val_score(lin_reg, housing_prepared, housing_labels, scoring="neg_mean_squared_error", cv=10)
pd.Series(np.sqrt(-scores)).describe()
>> count 10.000000
mean 69104.079982
std 3036.132517
min 64114.991664
25% 67077.398482
50% 68718.763507
75% 71357.022543
max 73997.080502
dtype: float64
모델 세부 튜닝
그리드 탐색
- 가능한 모든 조합에 대한 교차검증을 수행
- 조합이 커져서 많은 시간 소요
from sklearn.model_selection import GridSearchCV
param_grid = [
# 12(=3×4)개의 하이퍼파라미터 조합을 시도
{'n_estimators': [3, 10, 30], 'max_features': [2, 4, 6, 8]},
# bootstrap은 False로 하고 6(=2×3)개의 조합을 시도
{'bootstrap': [False], 'n_estimators': [3, 10], 'max_features': [2, 3, 4]},
]
forest_reg = RandomForestRegressor(random_state=42)
# 다섯 개의 폴드로 훈련하면 총 (12+6)*5=90번의 훈련
grid_search = GridSearchCV(forest_reg, param_grid, cv=5,
scoring='neg_mean_squared_error',
return_train_score=True)
grid_search.fit(housing_prepared, housing_labels)
>> GridSearchCV(cv=5, estimator=RandomForestRegressor(random_state=42),
param_grid=[{'max_features': [2, 4, 6, 8],
'n_estimators': [3, 10, 30]},
{'bootstrap': [False], 'max_features': [2, 3, 4],
'n_estimators': [3, 10]}],
return_train_score=True, scoring='neg_mean_squared_error')- 최상의 파라미터 조합
grid_search.best_params_
>> {'max_features': 8, 'n_estimators': 30}
grid_search.best_estimator_
>> RandomForestRegressor(max_features=8, n_estimators=30, random_state=42)- 그리드서치에서 테스트한 하이퍼파라미터 조합의 점수를 확인
cvres = grid_search.cv_results_
for mean_score, params in zip(cvres["mean_test_score"], cvres["params"]):
print(np.sqrt(-mean_score), params)
>> 63895.161577951665 {'max_features': 2, 'n_estimators': 3}
54916.32386349543 {'max_features': 2, 'n_estimators': 10}
52885.86715332332 {'max_features': 2, 'n_estimators': 30}
60075.3680329983 {'max_features': 4, 'n_estimators': 3}
52495.01284985185 {'max_features': 4, 'n_estimators': 10}
50187.24324926565 {'max_features': 4, 'n_estimators': 30}
58064.73529982314 {'max_features': 6, 'n_estimators': 3}
51519.32062366315 {'max_features': 6, 'n_estimators': 10}
49969.80441627874 {'max_features': 6, 'n_estimators': 30}
58895.824998155826 {'max_features': 8, 'n_estimators': 3}
52459.79624724529 {'max_features': 8, 'n_estimators': 10}
49898.98913455217 {'max_features': 8, 'n_estimators': 30}
62381.765106921855 {'bootstrap': False, 'max_features': 2, 'n_estimators': 3}
54476.57050944266 {'bootstrap': False, 'max_features': 2, 'n_estimators': 10}
59974.60028085155 {'bootstrap': False, 'max_features': 3, 'n_estimators': 3}
52754.5632813202 {'bootstrap': False, 'max_features': 3, 'n_estimators': 10}
57831.136061214274 {'bootstrap': False, 'max_features': 4, 'n_estimators': 3}
51278.37877140253 {'bootstrap': False, 'max_features': 4, 'n_estimators': 10}pd.DataFrame(grid_search.cv_results_)| mean_fit_time | std_fit_time | mean_score_time | std_score_time | param_max_features | param_n_estimators | param_bootstrap | params | split0_test_score | split1_test_score | ... | mean_test_score | std_test_score | rank_test_score | split0_train_score | split1_train_score | split2_train_score | split3_train_score | split4_train_score | mean_train_score | std_train_score | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.061683 | 0.001457 | 0.003252 | 0.000082 | 2 | 3 | NaN | {'max_features': 2, 'n_estimators': 3} | -4.119912e+09 | -3.723465e+09 | ... | -4.082592e+09 | 1.867375e+08 | 18 | -1.155630e+09 | -1.089726e+09 | -1.153843e+09 | -1.118149e+09 | -1.093446e+09 | -1.122159e+09 | 2.834288e+07 |
| 1 | 0.201465 | 0.002039 | 0.009988 | 0.000685 | 2 | 10 | NaN | {'max_features': 2, 'n_estimators': 10} | -2.973521e+09 | -2.810319e+09 | ... | -3.015803e+09 | 1.139808e+08 | 11 | -5.982947e+08 | -5.904781e+08 | -6.123850e+08 | -5.727681e+08 | -5.905210e+08 | -5.928894e+08 | 1.284978e+07 |
| 2 | 0.609780 | 0.003091 | 0.027216 | 0.000336 | 2 | 30 | NaN | {'max_features': 2, 'n_estimators': 30} | -2.801229e+09 | -2.671474e+09 | ... | -2.796915e+09 | 7.980892e+07 | 9 | -4.412567e+08 | -4.326398e+08 | -4.553722e+08 | -4.320746e+08 | -4.311606e+08 | -4.385008e+08 | 9.184397e+06 |
| 3 | 0.105176 | 0.001257 | 0.003308 | 0.000111 | 4 | 3 | NaN | {'max_features': 4, 'n_estimators': 3} | -3.528743e+09 | -3.490303e+09 | ... | -3.609050e+09 | 1.375683e+08 | 16 | -9.782368e+08 | -9.806455e+08 | -1.003780e+09 | -1.016515e+09 | -1.011270e+09 | -9.980896e+08 | 1.577372e+07 |
| 4 | 0.337638 | 0.002218 | 0.009668 | 0.000462 | 4 | 10 | NaN | {'max_features': 4, 'n_estimators': 10} | -2.742620e+09 | -2.609311e+09 | ... | -2.755726e+09 | 1.182604e+08 | 7 | -5.063215e+08 | -5.257983e+08 | -5.081984e+08 | -5.174405e+08 | -5.282066e+08 | -5.171931e+08 | 8.882622e+06 |
| 5 | 1.012371 | 0.001679 | 0.026792 | 0.000240 | 4 | 30 | NaN | {'max_features': 4, 'n_estimators': 30} | -2.522176e+09 | -2.440241e+09 | ... | -2.518759e+09 | 8.488084e+07 | 3 | -3.776568e+08 | -3.902106e+08 | -3.885042e+08 | -3.830866e+08 | -3.894779e+08 | -3.857872e+08 | 4.774229e+06 |
| 6 | 0.138414 | 0.001822 | 0.003374 | 0.000077 | 6 | 3 | NaN | {'max_features': 6, 'n_estimators': 3} | -3.362127e+09 | -3.311863e+09 | ... | -3.371513e+09 | 1.378086e+08 | 13 | -8.909397e+08 | -9.583733e+08 | -9.000201e+08 | -8.964731e+08 | -9.151927e+08 | -9.121998e+08 | 2.444837e+07 |
| 7 | 0.466506 | 0.002028 | 0.009475 | 0.000157 | 6 | 10 | NaN | {'max_features': 6, 'n_estimators': 10} | -2.622099e+09 | -2.669655e+09 | ... | -2.654240e+09 | 6.967978e+07 | 5 | -4.939906e+08 | -5.145996e+08 | -5.023512e+08 | -4.959467e+08 | -5.147087e+08 | -5.043194e+08 | 8.880106e+06 |
| 8 | 1.420788 | 0.008997 | 0.026797 | 0.000438 | 6 | 30 | NaN | {'max_features': 6, 'n_estimators': 30} | -2.446142e+09 | -2.446594e+09 | ... | -2.496981e+09 | 7.357046e+07 | 2 | -3.760968e+08 | -3.876636e+08 | -3.875307e+08 | -3.760938e+08 | -3.861056e+08 | -3.826981e+08 | 5.418747e+06 |
| 9 | 0.183978 | 0.002788 | 0.003376 | 0.000124 | 8 | 3 | NaN | {'max_features': 8, 'n_estimators': 3} | -3.590333e+09 | -3.232664e+09 | ... | -3.468718e+09 | 1.293758e+08 | 14 | -9.505012e+08 | -9.166119e+08 | -9.033910e+08 | -9.070642e+08 | -9.459386e+08 | -9.247014e+08 | 1.973471e+07 |
| 10 | 0.611858 | 0.004138 | 0.009630 | 0.000193 | 8 | 10 | NaN | {'max_features': 8, 'n_estimators': 10} | -2.721311e+09 | -2.675886e+09 | ... | -2.752030e+09 | 6.258030e+07 | 6 | -4.998373e+08 | -4.997970e+08 | -5.099880e+08 | -5.047868e+08 | -5.348043e+08 | -5.098427e+08 | 1.303601e+07 |
| 11 | 1.833474 | 0.007461 | 0.026732 | 0.000512 | 8 | 30 | NaN | {'max_features': 8, 'n_estimators': 30} | -2.492636e+09 | -2.444818e+09 | ... | -2.489909e+09 | 7.086483e+07 | 1 | -3.801679e+08 | -3.832972e+08 | -3.823818e+08 | -3.778452e+08 | -3.817589e+08 | -3.810902e+08 | 1.916605e+06 |
| 12 | 0.096498 | 0.001366 | 0.003925 | 0.000185 | 2 | 3 | False | {'bootstrap': False, 'max_features': 2, 'n_est... | -4.020842e+09 | -3.951861e+09 | ... | -3.891485e+09 | 8.648595e+07 | 17 | -0.000000e+00 | -4.306828e+01 | -1.051392e+04 | -0.000000e+00 | -0.000000e+00 | -2.111398e+03 | 4.201294e+03 |
| 13 | 0.319696 | 0.003882 | 0.010922 | 0.000064 | 2 | 10 | False | {'bootstrap': False, 'max_features': 2, 'n_est... | -2.901352e+09 | -3.036875e+09 | ... | -2.967697e+09 | 4.582448e+07 | 10 | -0.000000e+00 | -3.876145e+00 | -9.462528e+02 | -0.000000e+00 | -0.000000e+00 | -1.900258e+02 | 3.781165e+02 |
| 14 | 0.129983 | 0.002587 | 0.004045 | 0.000270 | 3 | 3 | False | {'bootstrap': False, 'max_features': 3, 'n_est... | -3.687132e+09 | -3.446245e+09 | ... | -3.596953e+09 | 8.011960e+07 | 15 | -0.000000e+00 | -0.000000e+00 | -0.000000e+00 | -0.000000e+00 | -0.000000e+00 | 0.000000e+00 | 0.000000e+00 |
| 15 | 0.434089 | 0.003336 | 0.011200 | 0.000206 | 3 | 10 | False | {'bootstrap': False, 'max_features': 3, 'n_est... | -2.837028e+09 | -2.619558e+09 | ... | -2.783044e+09 | 8.862580e+07 | 8 | -0.000000e+00 | -0.000000e+00 | -0.000000e+00 | -0.000000e+00 | -0.000000e+00 | 0.000000e+00 | 0.000000e+00 |
| 16 | 0.166674 | 0.001096 | 0.003801 | 0.000136 | 4 | 3 | False | {'bootstrap': False, 'max_features': 4, 'n_est... | -3.549428e+09 | -3.318176e+09 | ... | -3.344440e+09 | 1.099355e+08 | 12 | -0.000000e+00 | -0.000000e+00 | -0.000000e+00 | -0.000000e+00 | -0.000000e+00 | 0.000000e+00 | 0.000000e+00 |
| 17 | 0.544776 | 0.005262 | 0.011139 | 0.000471 | 4 | 10 | False | {'bootstrap': False, 'max_features': 4, 'n_est... | -2.692499e+09 | -2.542704e+09 | ... | -2.629472e+09 | 8.510266e+07 | 4 | -0.000000e+00 | -0.000000e+00 | -0.000000e+00 | -0.000000e+00 | -0.000000e+00 | 0.000000e+00 | 0.000000e+00 |
18 rows × 23 columns
랜덤 탐색
- 그리드 서치보다 적은 수의 조합을 수행할때 적절함
- 각 반복마다 하이퍼파라미터에 임의의 수를 대입, 지정된 횟수만큼 평가
- 랜덤 탐색을 1000 회 반복하면 하이퍼파라미터가 각기 다른 1000개의 값을 탐색
- 단순히 반복 횟수를 조절하는 것만으로 자원량 제어가능
from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import randint
param_distribs = {
'n_estimators': randint(low=1, high=200),
'max_features': randint(low=1, high=8),
}
forest_reg = RandomForestRegressor(random_state=42)
rnd_search = RandomizedSearchCV(forest_reg, param_distributions=param_distribs,
n_iter=10, cv=5, scoring='neg_mean_squared_error', random_state=42)
rnd_search.fit(housing_prepared, housing_labels)
>> RandomizedSearchCV(cv=5, estimator=RandomForestRegressor(random_state=42),
param_distributions={'max_features': <scipy.stats._distn_infrastructure.rv_frozen object at 0x7f6497a346d0>,
'n_estimators': <scipy.stats._distn_infrastructure.rv_frozen object at 0x7f6497660c50>},
random_state=42, scoring='neg_mean_squared_error')cvres = rnd_search.cv_results_
for mean_score, params in zip(cvres["mean_test_score"], cvres["params"]):
print(np.sqrt(-mean_score), params)
>> 49117.55344336652 {'max_features': 7, 'n_estimators': 180}
51450.63202856348 {'max_features': 5, 'n_estimators': 15}
50692.53588182537 {'max_features': 3, 'n_estimators': 72}
50783.614493515 {'max_features': 5, 'n_estimators': 21}
49162.89877456354 {'max_features': 7, 'n_estimators': 122}
50655.798471042704 {'max_features': 3, 'n_estimators': 75}
50513.856319990606 {'max_features': 3, 'n_estimators': 88}
49521.17201976928 {'max_features': 5, 'n_estimators': 100}
50302.90440763418 {'max_features': 3, 'n_estimators': 150}
65167.02018649492 {'max_features': 5, 'n_estimators': 2}
최상의 모델과 오차 분석
feature_importances = grid_search.best_estimator_.feature_importances_
feature_importances
>> array([6.96542523e-02, 6.04213840e-02, 4.21882202e-02, 1.52450557e-02,
1.55545295e-02, 1.58491147e-02, 1.49346552e-02, 3.79009225e-01,
5.47789150e-02, 1.07031322e-01, 4.82031213e-02, 6.79266007e-03,
1.65706303e-01, 7.83480660e-05, 1.52473276e-03, 3.02816106e-03])extra_attribs = ["rooms_per_hhold", "pop_per_hhold", "bedrooms_per_room"]
#cat_encoder = cat_pipeline.named_steps["cat_encoder"] # 예전 방식
cat_encoder = full_pipeline.named_transformers_["cat"]
cat_one_hot_attribs = list(cat_encoder.categories_[0])
attributes = num_attribs + extra_attribs + cat_one_hot_attribs
sorted(zip(feature_importances, attributes), reverse=True)
>> [(0.3790092248170967, 'median_income'),
(0.16570630316895876, 'INLAND'),
(0.10703132208204354, 'pop_per_hhold'),
(0.06965425227942929, 'longitude'),
(0.0604213840080722, 'latitude'),
(0.054778915018283726, 'rooms_per_hhold'),
(0.048203121338269206, 'bedrooms_per_room'),
(0.04218822024391753, 'housing_median_age'),
(0.015849114744428634, 'population'),
(0.015554529490469328, 'total_bedrooms'),
(0.01524505568840977, 'total_rooms'),
(0.014934655161887776, 'households'),
(0.006792660074259966, '<1H OCEAN'),
(0.0030281610628962747, 'NEAR OCEAN'),
(0.0015247327555504937, 'NEAR BAY'),
(7.834806602687504e-05, 'ISLAND')]
테스트 세트로 시스템 평가하기
final_model = grid_search.best_estimator_
X_test = strat_test_set.drop("median_house_value", axis=1)
y_test = strat_test_set["median_house_value"].copy()
X_test_prepared = full_pipeline.transform(X_test)
final_predictions = final_model.predict(X_test_prepared)
final_mse = mean_squared_error(y_test, final_predictions)
final_rmse = np.sqrt(final_mse)
final_rmse
>> 47873.26095812988- 테스트 RMSE에 대한 95% 신뢰 구간을 계산
from scipy import stats
confidence = 0.95
squared_errors = (final_predictions - y_test) ** 2
np.sqrt(stats.t.interval(confidence, len(squared_errors) - 1,
loc=squared_errors.mean(),
scale=stats.sem(squared_errors)))
>> array([45893.36082829, 49774.46796717])
연습문제 해답
1번
- 질문: 서포트 벡터 머신 회귀(sklearn.svm.SVR)를 kernel=“linear”(하이퍼파라미터 C를 바꿔가며)나 kernel=“rbf”(하이퍼파라미터 C와 gamma를 바꿔가며) 등의 다양한 하이퍼파라미터 설정으로 시도해보세요. 지금은 이 하이퍼파라미터가 무엇을 의미하는지 너무 신경 쓰지 마세요. 최상의 SVR 모델은 무엇인가요?
from sklearn.model_selection import GridSearchCV
param_grid = [
{'kernel': ['linear'], 'C': [10., 30., 100., 300., 1000., 3000., 10000., 30000.0]},
{'kernel': ['rbf'], 'C': [1.0, 3.0, 10., 30., 100., 300., 1000.0],
'gamma': [0.01, 0.03, 0.1, 0.3, 1.0, 3.0]},
]
svm_reg = SVR()
grid_search = GridSearchCV(svm_reg, param_grid, cv=5, scoring='neg_mean_squared_error', verbose=2)
grid_search.fit(housing_prepared, housing_labels)
>> Fitting 5 folds for each of 50 candidates, totalling 250 fits
[CV] END ..............................C=10.0, kernel=linear; total time= 6.3s
[CV] END ..............................C=10.0, kernel=linear; total time= 6.3s
[CV] END ..............................C=10.0, kernel=linear; total time= 6.2s
..............................
GridSearchCV(cv=5, estimator=SVR(),
param_grid=[{'C': [10.0, 30.0, 100.0, 300.0, 1000.0, 3000.0,
10000.0, 30000.0],
'kernel': ['linear']},
{'C': [1.0, 3.0, 10.0, 30.0, 100.0, 300.0, 1000.0],
'gamma': [0.01, 0.03, 0.1, 0.3, 1.0, 3.0],
'kernel': ['rbf']}],
scoring='neg_mean_squared_error', verbose=2)- 최상 모델의 5-폴드 교차 검증으로 평가한 점수
negative_mse = grid_search.best_score_
rmse = np.sqrt(-negative_mse)
rmse
>> 70286.61835383571- 최상의 하이퍼파라미터를 확인
grid_search.best_params_
>> {'C': 30000.0, 'kernel': 'linear'}선형 커널이 RBF 커널보다 성능이 더 좋음
C는 테스트한 것 중에 최대값이 선택
따라서 작은 값들은 지우고 더 큰 값의 C로 그리드서치를 다시 실행해 보면, 더 큰 값의 C에서 성능이 높아질 수도 있음
2번
- 질문: GridSearchCV를 RandomizedSearchCV로 바꿔보세요.
from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import expon, reciprocal
# expon(), reciprocal()와 그외 다른 확률 분포 함수에 대해서는
# https://docs.scipy.org/doc/scipy/reference/stats.html를 참고
# 노트: kernel 매개변수가 "linear"일 때는 gamma가 무시
param_distribs = {
'kernel': ['linear', 'rbf'],
'C': reciprocal(20, 200000),
'gamma': expon(scale=1.0),
}
svm_reg = SVR()
rnd_search = RandomizedSearchCV(svm_reg, param_distributions=param_distribs,
n_iter=50, cv=5, scoring='neg_mean_squared_error',
verbose=2, random_state=42)
rnd_search.fit(housing_prepared, housing_labels)
>> Fitting 5 folds for each of 50 candidates, totalling 250 fits
[CV] END C=629.782329591372, gamma=3.010121430917521, kernel=linear; total time= 6.3s
[CV] END C=629.782329591372, gamma=3.010121430917521, kernel=linear; total time= 6.2s
[CV] END C=629.782329591372, gamma=3.010121430917521, kernel=linear; total time= 6.3s
[CV] END C=629.782329591372, gamma=3.010121430917521, kernel=linear; total time= 6.2s
.....................
RandomizedSearchCV(cv=5, estimator=SVR(), n_iter=50,
param_distributions={'C': <scipy.stats._distn_infrastructure.rv_frozen object at 0x7f64a0e793d0>,
'gamma': <scipy.stats._distn_infrastructure.rv_frozen object at 0x7f64a0e79c90>,
'kernel': ['linear', 'rbf']},
random_state=42, scoring='neg_mean_squared_error',
verbose=2)- 최상 모델의 5-폴드 교차 검증으로 평가한 점수
negative_mse = rnd_search.best_score_
rmse = np.sqrt(-negative_mse)
rmse
>> 54751.69009488048- 최상의 하이퍼파라미터를 확인
rnd_search.best_params_
>> {'C': 157055.10989448498, 'gamma': 0.26497040005002437, 'kernel': 'rbf'}
3번
- 질문: 가장 중요한 특성을 선택하는 변환기를 준비 파이프라인에 추가해보세요.
- np.partition(list, int) -> list
- (list, 2)와 같은 경우는 리스트에서 순서 상관없이 작은 숫자 2개를 뽑아 왼쪽으로 놓겠다는 의미
- (list, -2)와 같은 경우는 리스트에서 순서 상관없이 큰 값 2개를 뽑아 오른쪽으로 놓겠다는 의미이다.
- np.argpartition 는 np.partition 와 같지만 index를 반환
from sklearn.base import BaseEstimator, TransformerMixin
def indices_of_top_k(arr, k):
return np.sort(np.argpartition(np.array(arr), -k)[-k:])
class TopFeatureSelector(BaseEstimator, TransformerMixin):
def __init__(self, feature_importances, k):
self.feature_importances = feature_importances
self.k = k
def fit(self, X, y=None):
self.feature_indices_ = indices_of_top_k(self.feature_importances, self.k)
return self
def transform(self, X):
return X[:, self.feature_indices_]- 선택할 특성의 개수를 지정
k = 5- 최상의 k개 특성의 인덱스를 확인
top_k_feature_indices = indices_of_top_k(feature_importances, k)
top_k_feature_indices
>> array([ 0, 1, 7, 9, 12])
np.array(attributes)[top_k_feature_indices]
>> array(['longitude', 'latitude', 'median_income', 'pop_per_hhold',
'INLAND'], dtype='<U18')- 최상의 k개 특성이 맞는지 다시 확인
sorted(zip(feature_importances, attributes), reverse=True)[:k]
>> [(0.3790092248170967, 'median_income'),
(0.16570630316895876, 'INLAND'),
(0.10703132208204354, 'pop_per_hhold'),
(0.06965425227942929, 'longitude'),
(0.0604213840080722, 'latitude')]- 이전에 정의한 준비 파이프라인과 특성 선택기를 추가한 새로운 파이프라인 생성
preparation_and_feature_selection_pipeline = Pipeline([
('preparation', full_pipeline),
('feature_selection', TopFeatureSelector(feature_importances, k))
])
housing_prepared_top_k_features = preparation_and_feature_selection_pipeline.fit_transform(housing)- 처음 3개 샘플의 특성
housing_prepared_top_k_features[0:3]
>> array([[-0.94135046, 1.34743822, -0.8936472 , 0.00622264, 1. ],
[ 1.17178212, -1.19243966, 1.292168 , -0.04081077, 0. ],
[ 0.26758118, -0.1259716 , -0.52543365, -0.07537122, 1. ]])- 최상의 k개 특성이 맞는지 다시 확인
housing_prepared[0:3, top_k_feature_indices]
>> array([[-0.94135046, 1.34743822, -0.8936472 , 0.00622264, 1. ],
[ 1.17178212, -1.19243966, 1.292168 , -0.04081077, 0. ],
[ 0.26758118, -0.1259716 , -0.52543365, -0.07537122, 1. ]])
4번
- 질문: 전체 데이터 준비 과정과 최종 예측을 하나의 파이프라인으로 만들어보세요.
rnd_search.best_params_
>> {'C': 157055.10989448498, 'gamma': 0.26497040005002437, 'kernel': 'rbf'}prepare_select_and_predict_pipeline = Pipeline([
('preparation', full_pipeline),
('feature_selection', TopFeatureSelector(feature_importances, k)),
('svm_reg', SVR(**rnd_search.best_params_))
])
prepare_select_and_predict_pipeline.fit(housing, housing_labels)
>> Pipeline(steps=[('preparation',
ColumnTransformer(
transformers=[('num', Pipeline(steps=[('imputer',
SimpleImputer(strategy='median')),
('attribs_adder', CombinedAttributesAdder()),
('std_scaler', StandardScaler())]),
['longitude', 'latitude',
'housing_median_age',
'total_rooms',
'total_bedrooms',
'population', 'households',
'median_income']),
('cat', OneHotEncoder(...
TopFeatureSelector(feature_importances=array([...]), k=5)),
('svm_reg', SVR(C=157055.10989448498, gamma=0.26497040005002437))])- 몇 개의 샘플에 전체 파이프라인을 적용
some_data = housing.iloc[:4]
some_labels = housing_labels.iloc[:4]
print("Predictions:\t", prepare_select_and_predict_pipeline.predict(some_data))
print("Labels:\t\t", list(some_labels))
>> Predictions: [ 83384.49158095 299407.90439234 92272.03345144 150173.16199041]
Labels: [72100.0, 279600.0, 82700.0, 112500.0]
5번
- 질문: GridSearchCV를 사용해 준비 단계의 옵션을 자동으로 탐색해보세요.
full_pipeline.named_transformers_["cat"].handle_unknown = 'ignore'
param_grid = [{
'preparation__num__imputer__strategy': ['mean', 'median', 'most_frequent'],
'feature_selection__k': list(range(1, len(feature_importances) + 1))
}]
grid_search_prep = GridSearchCV(prepare_select_and_predict_pipeline, param_grid, cv=5,
scoring='neg_mean_squared_error', verbose=2)
grid_search_prep.fit(housing, housing_labels)
>> Fitting 5 folds for each of 48 candidates, totalling 240 fits
[CV] END feature_selection__k=1, preparation__num__imputer__strategy=mean; total time= 10.4s
[CV] END feature_selection__k=1, preparation__num__imputer__strategy=mean; total time= 9.9s
[CV] END feature_selection__k=1, preparation__num__imputer__strategy=mean; total time= 9.9s
[CV] END feature_selection__k=1, preparation__num__imputer__strategy=mean; total time= 9.8s
[CV] END feature_selection__k=1, preparation__num__imputer__strategy=mean; total time= 9.9s
.....
GridSearchCV(cv=5, estimator=Pipeline(steps=[('preparation',
ColumnTransformer(transformers=[('num', Pipeline(steps=[('imputer',
SimpleImputer(strategy='median')),
('attribs_adder', CombinedAttributesAdder()),
('std_scaler', StandardScaler())]),
['longitude', 'latitude', 'housing_median_age',
'total_rooms', 'total_bedrooms', 'population',
'households','median_inc...]), k=5)),
('svm_reg', SVR(C=157055.10989448498, gamma=0.26497040005002437))]),
param_grid=[{'feature_selection__k': [1, 2, 3, 4, 5, 6, 7, 8, 9,
10, 11, 12, 13, 14, 15, 16],
'preparation__num__imputer__strategy': ['mean',
'median',
'most_frequent']}],
scoring='neg_mean_squared_error', verbose=2)- 최적의 파라미터 찾기
grid_search_prep.best_params_
>> {'feature_selection__k': 1, 'preparation__num__imputer__strategy': 'mean'}'Study > Self Education' 카테고리의 다른 글
| 핸즈온 머신러닝 - 6 (0) | 2024.06.18 |
|---|---|
| 핸즈온 머신러닝 - 5 (0) | 2024.06.17 |
| 핸즈온 머신러닝 - 4 (2) | 2024.06.17 |
| 핸즈온 머신러닝 - 3 (1) | 2024.06.15 |
| 핸즈온 머신러닝 - 1 (1) | 2024.06.13 |
